서 론
식품의 가열처리공정
가열사멸공정
가열살균공정에서 품질의 변화
가열처리공정의 지배방정식
시뮬레이션 모델의 식품의 가열살균공정의 적용 사례
고체 식품과 고점도의 액상 식품
액상 식품
액상과 고체상이 혼합된 식품
가열 살균공정에서의 시뮬레이션의 한계와 미래
결 론
서 론
가공식품의 제조 시 유통기한의 연장을 위한 고온 또는 저온살균과정은 필수적인 단위조작 중의 하나로 인식되고 있다(Stumbo et al., 1975). 가열처리공정은 과일, 야채, 우유, 생선, 고기 등의 다양한 식품과 식품소재의 유통기한을 연장하기 위하여 가장 범용적으로 사용되는 공정이다. 비가열처리공정은 지난 십 수 년 간 많은 진보를 이루었으나 실질적으로 산업체에서는 가열처리공정이 살균의 요한 기작으로 사용되고 있다. 가열처리 공정은 포화증기(steam)나 열수(hot water)를 열전달의 매질로 사용하여 일정한 압력 하에서 식품에 열전달매질을 노출시켜 식품의 유통기한을 연장시키기 위하여 미생물을 사멸하는 공정이다. 이와 같은 가열처리 공정은 일반적으로 식품을 용기에 포장한 후에 적용되며 식품과 용기의 열적특성과 형상에 따라 가열처리 공정의 인자들이 결정지어진다.
식품의 가열처리 공정의 설계에서 가장 중요한 요인은 가열처리 공정 중 식품 내부의 냉점(cold point, CP)이나 냉지역(slowest heating zone, SHZ)를 정확하게 찾는 것이다. CP나 SHZ는 가열 도중 식품의 온도가 가장 늦게 상승하는 지점을 의미하며 식품 내의 미생물을 목표하는 정도로 살균하기 위해서는 CP나 SHZ에서의 누적온도효과가 설정한 온도에 충분히 도달하여야 한다(Singh et al., 2015). 가열 중 온도가 CP나 SHZ에 목표한 만큼 도달하지 않을 경우 미생물의 사멸이 충분하지 않아 유통기한의 확보가 어려우며, 또한 CP나 SHZ가 잘못 설정되어 필요 이상의 열이 공급될 경우 과도한 품질의 변화와 에너지 손실이 발생한다. 특히 열처리 공정을 핵심기술로 사용하는 통조림 및 상온식품가공업체의 경우 최적의 살균 온도 및 시간을 찾는 것이 기술적으로 가장 중요한 요인으로 인식되고 있다(Ghani et al., 2002). 그러므로 식품과 포장용기의 다양한 형상과 크기에 따라 열전달 이론을 적용하여 정확한 CP나 SHZ를 설정하고 이에 따른 살균 온도와 시간을 규정하는 것은 열처리공정의 핵심이 되는 설계요소이다(Lee and Yoon, 2016).
그 중요도에도 불구하고, 실질적인 열처리 공정 중 정교한 CP를 설정하고 이에 따른 살균 온도와 시간을 규정하는 수학적 모델을 개발하는 과정은 매우 어려운 일이다. 다양한 용기의 형상에 따른 열전달 속도를 추론하는 일도 매우 복잡한 계산을 요구하며, 무엇보다 자연대류(natural convection) 현상은 액상 또는 고형분이 포함된 액상 식품의 CP를 설정하는 수학적 모델을 개발하는데 매우 큰 어려움을 준다(Dimou and Yanniotis, 2011). 용기 내에서 비정상상태의 온도구배를 나타내기 위해서는 에너지식과 운동량식을 동시에 풀어야 하며 이때 부력의 영향을 받는 자연대류의 생성과 영향은 가열 도중 CP를 지속적으로 이동 시키므로 용기 내의 비정상상태의 온도구배를 계산하는데 어려운 요소로 작용하게 된다. 이와 같이 변화되는 CP의 영향을 국부적으로 안배하여 특정 지점이 아닌 특정 영역에서 온도가 가장 늦게 상승하는 SHZ를 설정하는 것이 CP를 대체하여 액상식품에서의 가열공정을 설계하는 일반적인 방법이나 국부적인 영역을 설정하는 것 역시 해석적인 해를 구하는 방법으로는 설정하기가 매우 어려우며 실험적으로도 많은 시행착오를 요구하는 영역이다.
가열처리 과정 중 변화되는 비정상상태의 온도구배를 나타내기 위하여 수학적 모델의 필요성이 인지되어 왔으며, 수학적 모델은 실험으로 측정한 온도(열침투곡선)와의 비교로 모델의 타당성이 검증되었다. F-value는 온도의 누적효과에 따른 살균도를 나타내는 일반적인 지표로 사용되며, CP나 SHZ를 설정하기 위해서는 열침투곡선을 바탕으로 환산된 특정 지점의 F-value의 변화를 지표로 사용하여야 가열처리 공정의 조건과 살균도의 관계를 규정지을 수 있게 된다. 이와 같이 수학적 모델과 실험적인 열침투곡선의 관계를 바탕으로 살균정도를 예측하기 위한 연구는 원형의 통조림에서 비정상상태에서의 속도와 온도구배를 수학적으로 예측하고 이에 따른 살균도를 적용하는 방법을 발표한 Datta and Teixeira (1988)에 의하여 체계적으로 개발되었다. 수학적 모델의 타당성이 검증되고 컴퓨터의 계산수행능력이 증대됨에 따라 Kumar et al. (1990)에 의하여 열처리공정의 컴퓨터시뮬레이션 모델개발에 관련된 연구가 진전되어졌다(Kumar et al., 1991). 컴퓨터 시뮬레이션은 최근 다양한 식품의 가열처리 공정에 응용되어 공정의 설계와 최적화에 활용되고 있다(Bhuvaneswari and Anandharamakrishnan, 2014; Erdogdu et al., 2010; Ghani and Farid, 2005; Kiziltas et al., 2010; Koribilli et al., 2011; Lespinard and Mascheroni, 2012; Rawajfeh et al., 2013; Shafiekhani et al., 2016; Spanu and Vignali, 2016).
본 총설의 목적은 최근 급격히 증가하는 컴퓨터를 이용하여 열전달모델을 적용하여 식품의 열처리 공정의 설계와 최적화에 관련된 연구와 이를 위해 선행적으로 학습되어야 할 식품의 가열살균이론을 제시함에 있다. 본 총설에는 식품의 가열처리 공정 중에 사용되는 기본적인 열전달 지배방정식과 유체흐름의 지배방정식과 최근 개발된 모델들에 대한 고찰을 포함하였으며 식품의 다양한 상(예, 고상, 액상, 및 고상과 액상의 혼합물)에 적용한 사례를 포함하여 기술하였다. 최종적으로 컴퓨터시뮬레이션의 최근 동향과 한계점을 간략히 소개하였다.
식품의 가열처리공정
가열사멸공정
가열사멸 공정 중의 생존하는 미생물의 숫자는 일반적으로 로그수준으로 감소된다. 이와 같은 로그수준의 감소는 가열시간에 관계없이 미생물을 100% 사멸하는 멸균(sterilization)에 도달하는 것이 이론적으로 불가능함을 말해준다. 그러나 미생물의 생존은 확률적으로 표현되며 충분히 안정적인 유통을 하기 위한 사멸정도(살균도)를 주어진 초기의 미생물조건과 가열살균 온도와 시간으로 확률적으로 계산할 수 있다.
미생물의 사멸은 일반적으로 1차 반응으로 표현할 수 있다. 주어진 특정온도에서 미생물의 수를 지수로 표현할 경우 시간에 따른 로그수준의 감소로 표현할 수 있으며, 이와 같은 그래프를 ‘생존곡선’이라 부르며 일반적인 형태는 Fig. 1과 같다.
미생물의 수를 90%로 감소시킬 때 필요한 시간을 D-value (decimal reduction time, DT)이라고 하며 특정 미생물에 대한 살균의 중요한 지표로 사용하고 있다. 또한 D-value는 온도의 함수로서 온도의 증가에 따라 그 값이 감소하게된다. 생존곡선과 유사하게 종속변수(D-value)와 독립변수(온도)를 semi-log scale로 작도 시 온도에 따라 종속변수는 선형적으로 감소하는 모습을 보여준다(Fig. 2). 이때 1 log 수준의 감소를 가져올 수 있는 온도를 Z-value라고 부른다. Z-value는 온도의 변화가 살균시간에 미치는 영향을 주는 중요한 인자로 활용된다.
F-value는 가열살균공정에서 가장 중요한 값으로, 특정한 온도에서 식품 내의 미생물을 가열살균을 통하여 안전하게 유통시키기 위하여 목적하는 양만큼 미생물을 감소시키는 데 필요한 시간을 의미한다. 특정한 기준온도(Tref)에서의 F-value는 Z-value와 시간에 따른 온도변화곡선의 값을 통하여 식 (1)로 계산된다.
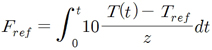 (1)
(1)
가열살균공정을 통하여 안정적인 유통기한을 확보하기 위해서는 해당 식품이 목표로 하는 F-value를 살균과정의 온도변화곡선과 식 (1)을 통하여 얻은 F-value로 만족시켜야 한다.
가열살균공정에서 품질의 변화
서론에서 이야기된 바와 같이 가열살균공정은 식품의 품질변화를 동반한다. 가열 시의 식품의 품질변화도 생화학적 반응의 일부이므로 화학반응식으로 표현될 수 있다. 실제로 식품 내에서 발생하는 화학변화는 매우 복잡하지만, 일반적으로 가열살균 시에 발생할 수 있는 효소반응, 미생물의 불확성, 품질(향, 색, 및 조직감), 영양성분의 변화는 1차 반응식으로 표현될 수 있다(Hartel and Heldman, 1997). 1차 반응에서 변화속도는 각 요인의 농도에 비례하며 이는 식 (2)와 같이 표현할 수 있다.
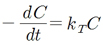 (2)
(2)
식 (2)의 미분방정식표현은 특정한 가열 살균시간 중의 변화로 적분을 하여 반응속도상수(kT)를 식 (3)과 같이 도출 할 수 있다.
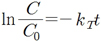 (3)
(3)
반응속도상수(kT)와 DT와는 유사한 개념으로 kT는 품질의 변화속도를 나타내는 인자이며 DT는 미생물의 감소속도를 나타내는 인자로 사용된다. 반응상수가 미생물의 가열에 의한 살균과정에 적용될 경우 kT와 DT는 다음과 같은 관계를 가진다.
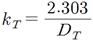 (4)
(4)
반응속도상수(kT)는 온도의존적이며 반응속도상수의 온도의존성은 일반적으로 Arrhenius식을 통하여 표현된다.
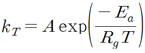 (5)
(5)
DT와 F-value는 가열살균공정에서 특정한 병원균을 불활성화 시키는 정도를 나타내는 중요한 인자로 사용되며, 특히 살균온도와 살균시간을 규정지어 살균공정을 설계하는데 매우 중요한 역할을 한다. 그러나 이 두 인자를 직접적으로 사용하여 식품의 살균공정을 완전히 설계하는데는 매우 큰 어려움이 있다. 그 이유는 식품 내부의 온도는 식품내부의 열저항에 의한 온도구배가 존재하며 식품의 살균과정은 전형적인 비정상상태의 열전달 과정이므로 특정한 시간과 장소에서의 온도를 예측하여야만 DT와 F-value를 적용하여 살균공정을 정확하게 설계할 수 있다.
가열처리공정의 지배방정식
유체의 운동방정식은 약 2세기전 완성되어 사용되고 있다(Euler, 1761). Euler식의 경우 질량, 에너지, 그리고 운동량 보존법칙을 근간으로 유도되어 1756-1757년경 완성되어졌다. Euler식에 응력 텐서를 적용시켜 보다 광범위하게 유체의 운동을 나타낼 수 있는 Navier-Stokes식이 완성되어 범용적인 유체의 흐름을 나타내는 지배방정식으로 사용되고 있다(Navier, 1823; Stokes, 1851). Navier-Stokes식은 현대의 컴퓨터시뮬레이션을 통한 유체현상의 해석에 기본적인 식으로 사용되고 있다(Lee and Yoon, 2014). 가열처리 공정에 사용되는 지배방정식들은 다음과 같다.
에너지 식: 공간의 미소체적에서의 에너지의 변화속도는 일과 열의 출입에 따라 식 (6)과 같이 표현된다.
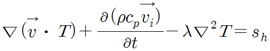 (6)
(6)
연속 방정식: 공간상의 미소체적을 출입하는 질량은 동일하여야 하며, 이에 따라 식 (7)과 같이 표현된다.
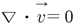 (7)
(7)
운동량 방정식: 공간상의 미소체적에 출입하는 선형운동량의 변화량은 식 (8)과 같이 표현된다.
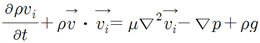 (8)
(8)
유체의 운동 중 부력에 의한 밀도가 변화되는 운동의 경우 운동량방정식에 Boussinesq 가정을 포함하여 사용한다. Boussinesq가정은 식 (9)와 같다.
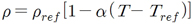 (9)
(9)
고체나 고체와 액체의 혼합물의 살균공정에 컴퓨터 시뮬레이션을 적용시키기 위해서는 고체에 적용되는 열전달 방정식을 포함해야한다(Cordioli et al., 2014; Mosna and Vignali, 2015; Park and Yoon, 2018). 이와 같이 고체에 적용되는 열전달방정식은 식 (6)에서 유체의 대류효과에 의한 항을 제거하여 식 (10)과 같이 표현된다.
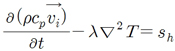 (10)
(10)
시뮬레이션 모델의 식품의 가열살균공정의 적용 사례
통조림용기 안의 식품의 가열공정의 해석에 대하여 축-대칭성을 이용한 계산시간을 단축하는 시뮬레이션 모델은 Tutlar and Erdogdu (2012)에 의하여 개발되었다. 축-대칭성을 이용한 모델은 수직과 수평의 원통형 용기에서의 3차원의 열전달 해석을 2차원 상태에서 가능하게 하여 정교한 해를 얻는데 걸리는 시간에 대한 단축이 가능하게 하였다. 이와 같은 축-대칭성의 시뮬레이션 모델에 대한 실질적인 적용은 용기의 형상과 가열 살균 시의 용기의 방향에 따라 적용이 가능한지의 여부가 결정되는 단점을 가지고 있다. 특히 축-대칭성 모델을 적용할 경우 격자(mesh) 품질과 적용 시간 등의 다양한 시뮬레이션 인자들에 보다 민감한 영향을 받는다. 이와 같은 민감도를 고려하여 수치적 접근법(numerical scheme)은 1차 hybrid방식을 사용하여 가열 살균해석 시의 수렴조건을 만족시키는 방법이 제안되었으며, 이와 함께 격자품질의 우수성이 항상 해의 정밀성을 보장하지는 않는 다는 것이 보고되었다(Norton and Sun, 2006). 특히 높은 격자품질이 오히려 시뮬레이션 초기 시 온도의 변동성을 가져와 시뮬레이션을 저해하는 요인이 될 수 있음을 보고 하였다.
가열살균 공정에서 시뮬레이션의 주된 역할은 살균 공정 중 포장용기내의 유체의 흐름과 이에 따른 온도분포를 계산하고 이를 바탕으로 가열살균공정을 해석하는 것이다. 이와 같은 수치적인 해석을 통하여 살균공정에 적용되는 온도와 살균 시간을 예측하는 것이 가능하므로 살균공정의 최적설계에 매우 중요한 역할을 하게 된다.
고체 식품과 고점도의 액상 식품
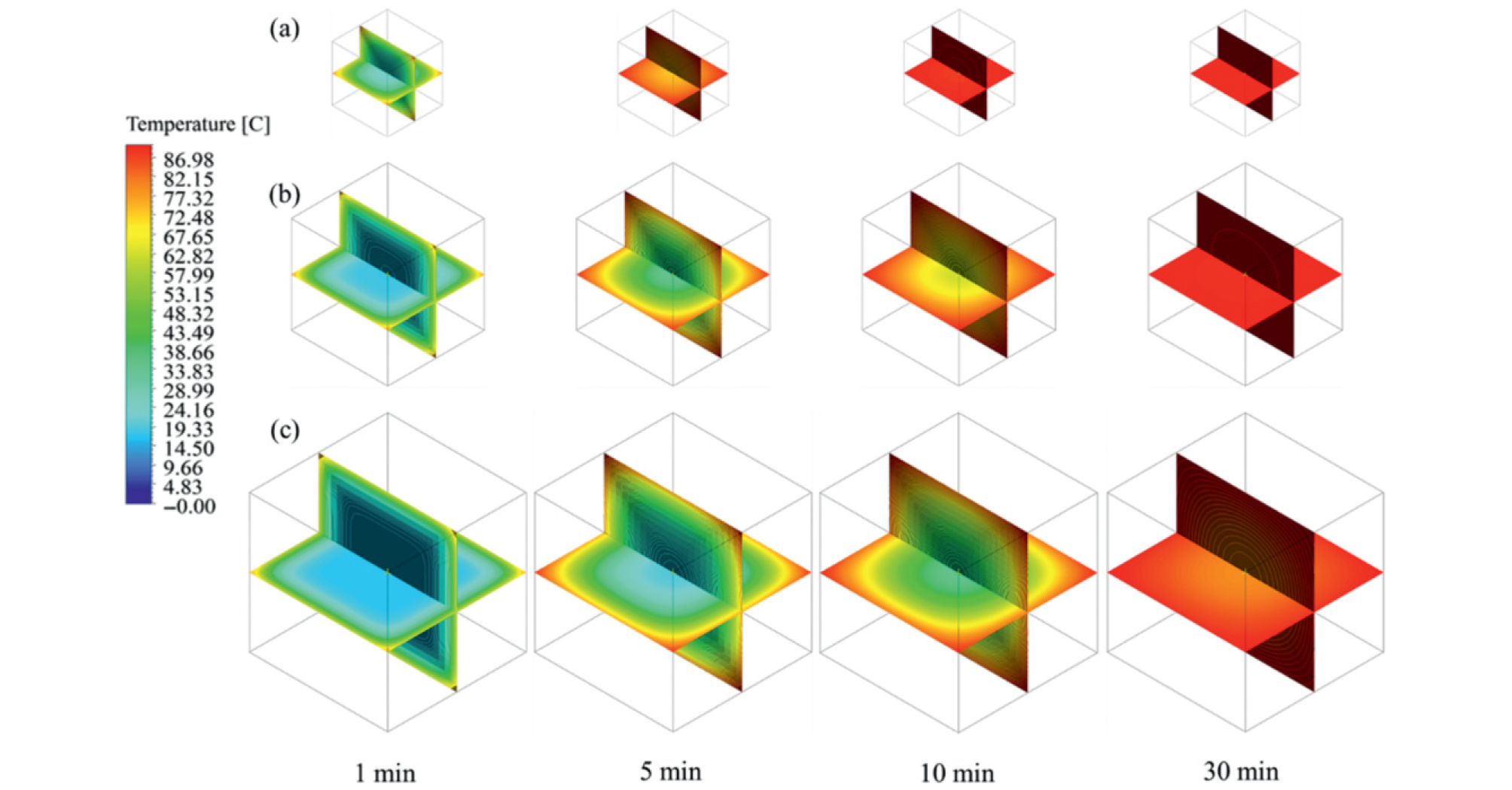
살균공정을 설계함에 있어서 가장 선행되어야 하는 과정은 가열되는 제품의 냉점(cold point, CP) 또는 최저가열영역(slowest heating zone, SHZ)을 설정하는 것이다. 살균공정의 설계의 기본 요소인 살균온도와 살균시간은 CP나 SHZ에서 목표로하는 살균도를 만족할 정도의 온도와 시간을 의미하는 것이다. 살균하고자 하는 식품의 가열시간과 온도는 안전하게 유통하기 위하여 충분한 미생물의 사멸과 함께 품질의 변화를 최소화하는 상태로 설계되어야 하며, 이때 살균온도는 CP나 SHZ를 기준으로 그 지점이 살균온도에 도달한 후의 시간 또는 그 지점의 누적살균도를 바탕으로 설정되어야 한다. 일반적으로 고체식품의 경우 전도(conduction)가 주된 열전달기작이므로 CP는 가열하고자 하는 식품의 기하학적 중심에 위치하며 실험적인 방법으로 쉽게 CP의 위치를 찾을 수 있다(Pflug, 1975). 또한 고점도의 액상식품의 경우도 고체식품과 유사하게 전도가 주된 열전달기작이므로 CP를 실험적으로 구하는 것이 가능하다. 최근 고점도 유체 식품의 정교한 열전달현상을 시뮬레이션하기 위한 다양한 연구가 진행되고 있다(Vatankhah et al., 2015). Shafiekhani et al. (2016)은 사과 퓨레의 가열처리 공정에서의 열전달현상을 해석하기 위하여 격자품질에 따른 온도구배와 SHZ의 위치변화를 정교하게 예측하는 수치해석모델을 개발하였다. 생선의 근섬유단백질로 이루어진 수리미반죽은 유체상태에서 매우 높은 점도를 지닌 전형적인 고점도 유체특성을 지닌다. Lee and Yoon (2016)은 수리미반죽의 열전달을 시뮬레이션하는 과정 중 단백질의 열변성이 미치는 영향을 고찰하였다. 수리미반죽은 생선의 근섬유단백질(myofibrillar protein)을 다량 함유하고 있으므로 가열처리 시 단백질에 의한 상변화가 수반되며, 이 sol-gel상변화를 일으키는 단백질 변성에 필요한 에너지를 고려한 시뮬레이션 모델이 필요함을 실험과 시뮬레이션결과를 비교하여 제안하였다. 이 연구에서는 sol-gel상변화를 포함한 시뮬레이션모델이 상변화를 포함하지 않은 모델에 비하여 실험값과 비교 시 매우 정교한 온도분포를 보여주는 것을 확인하였다(Fig. 3).
액상 식품
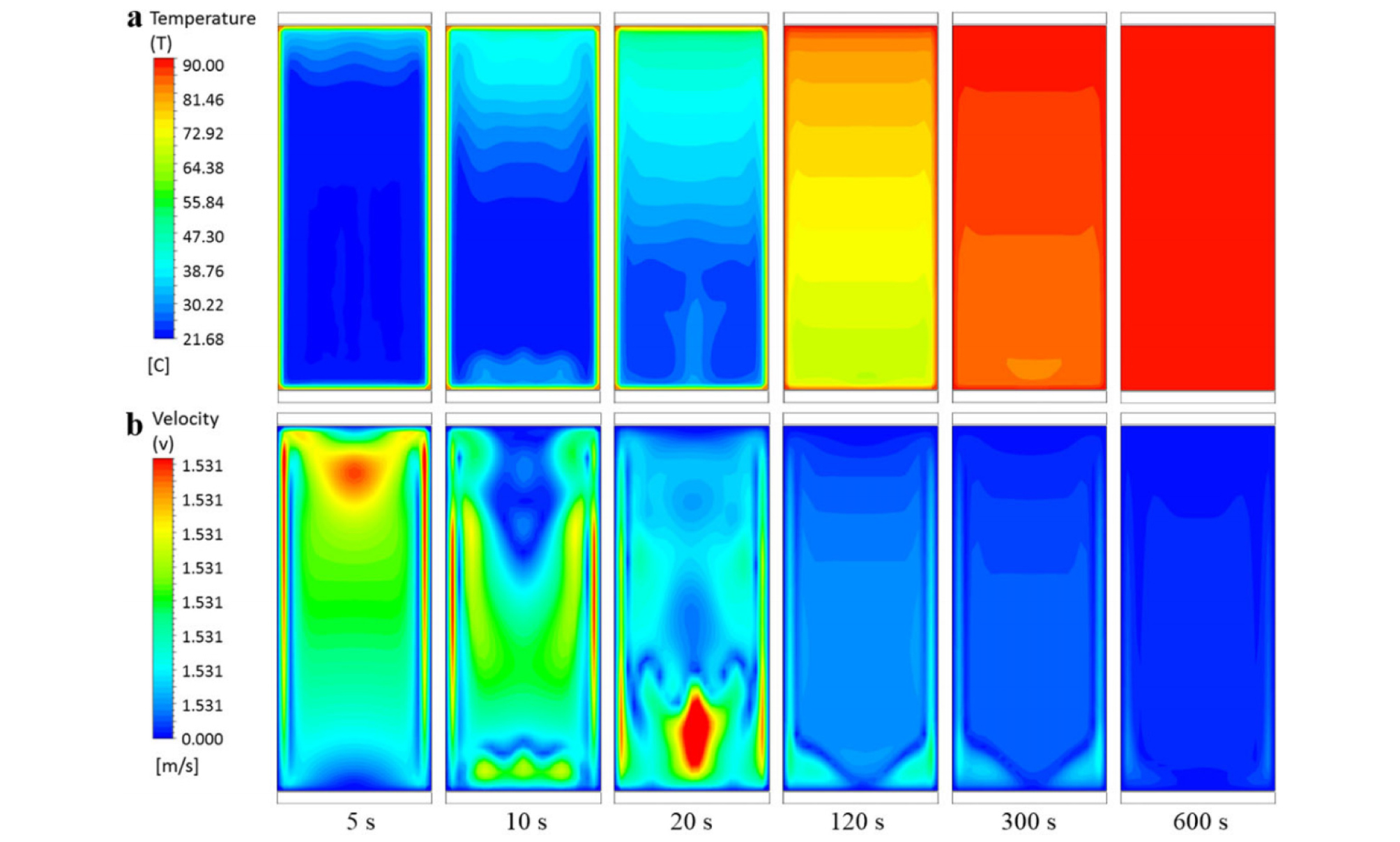
고체식품과는 달리 액상의 식품은 CP를 결정하는 것이 매우 어렵다. 액체의 경우 가열되는 동안 온도차이에 의한 밀도의 변화로 인하여 지속적인 유동(자연대류)이 발생한다. 그러므로 용기 안의 액상 식품의 경우 가열처리동안 온도의 변화와 함께 유체의 지속적인 이동이 발생한다(Rao and Anantheswaran, 1988). 시뮬레이션은 이와 같은 액체의 유동과 함께 변화되는 온도구배를 예측하기 위하여 많이 사용되며 매우 효과적인 방법으로 인정되고 있다(Scott and Richardson, 1997). 특히 용기 안의 액상 식품이 가열 도중 생성하는 자연대류 현상은 에너지 수지식과 함께 운동량 수지식을 동시에 반영하여야만 부력에 의하여 생성되는 유체의 흐름과 온도분포를 정확하게 예측할 수가 있다. 원통형 용기 안의 액상식품이 가열살균 도중 발생하는 유체의 흐름은 Lee and Yoon (2014)에 의하여 표준화된 방법으로 해석되었다(Fig. 4). 가열 초기 단계에서는 벽면에 가까이 있는 유체는 no-slip경계 조건에 따라 정지되어 있는 유체의 특성을 지니게 되며, 가열이 진행됨에 따라 벽면 근처의 유체는 전도에 의한 열전달 기작(즉, 벽면온도와 벽면 근처의 유체의 온도가 동일)이 주가 되나 용기의 중심에 있는 유체의 경우 여전히 초기 온도를 유지한 상태가 일정한 시간 동안 지속된다. 가열이 지속적으로 진행되는 동안 높은 온도의 유체는 밀도가 낮아지며 이에 따라 밀도의 차이에 의한 부력이 발생하여 용기 내에서 유동이 발생하게 된다. 이와 같은 유동은 속도장을 생성하게 되며 이는 유체의 점성력과 유체의 부력간의 힘의 비에 의하여 결정된다. 또한 온도가 상승함에 따라 유체의 점도는 일반적으로 낮아지게 되며 이는 용기 내 유체의 유동을 가속화 시키는 원인이 된다. 부력은 용기내의 유에의 온도가 균일한 상태로 평형에 도달하게 되면 사라지게 되고 이는 용기 내의 유동 속도를 줄이고 궁극적으로 유동을 멈추게 한다(Kumar and Bhattacharya, 1991).
가열 살균 공정 중의 용기 내 액상 식품이 생성하는 유동현상과 SHZ의 위치를 결정하기 위하여 시뮬레이션은 다양한 식품(예, 맥주, carboxy-methyl cellulose (CMC), 체리 주스, 옥수수 전분용액, soup, 대두유, 우유)에 사용되어 왔다(Augusto et al., 2010; Chen et al., 2005; Erdogdu et al., 2010; Ghani et al., 1999; Koribilli et al., 2011; Lee and Yoon, 2014; Moraga et al., 2011; Paul, 2011; Rawajfeh et al., 2013; Siriwattanayotin et al., 2006). 이와 같은 유동현상과 열전달의 해석에 사용되는 시뮬레이션은 액상 식품의 가열 살균공정의 설계에 필요한 살균온도와 살균시간을 결정하는데 매우 효율적으로 이용된다. 추가적으로 원통형의 용기 내부의 액상식품의 유체의 거동과 온도분포를 액상 식품의 점도와 용기의 크기에 따라 변화되는 상관관계를 도출하는 연구도 Farid and Ghani (2004)에 의하여 이루어 졌다.
용기가 정지되지 않은 교반되는 상태에서의 유체의 흐름과 열전달 현상에 대한 해석도 시뮬레이션을 통하여 시도되었다. Ghani et al. (2002)에 따르면 용기를 회전 시킬 시 SHZ에서의 열전달 속도는 정지된 상태에 비하여 4배 이상 증가함을 보여주었다. Erdogdu and Tutar (2011)는 유한체적법을 도입하여 가열 살균 도중 원통형 용기의 회전속도와 물리적인 특성이 열전달 속도에 주는 영향을 분석하였다. 온도가 증가할수록 회전속도가 열전달 속도에 주는 드는 것이 확인되었다. 또한 2개의 상(기체-식품, 기체-물)이 담겨 있는 수평형 용기가 회전할 경우 흐름의 특성과 열전달 특성도 Turtar and Erdogdu (2012)에 의하여 연구되었다. 이와 같은 2개의 상이 있는 경우 회전 속도에 의하여 흐름의 특성이 유의미하게 변화됨을 확인하였다. 특히 이와 같은 2개의 상이 존재하는 경우 기포가 액체 내에서 유동하는 과정에 대한 해석이 수치적으로 이루어졌다(Erdogdu and Tutar, 2011; Tutar and Erdogdu, 2012). 용기 내의 식품과 용기 상층부와의 공간(head space)의 여부는 기포의 생성에 영향을 주며 그 생성된 기포는 흐름에 영향을 주게 됨을 보고하였다.
가열 공정 도중 용기 내의 유체의 흐름은 용기의 형상에 많은 영향을 받게 된다. 매우 작은 형상의 변화도 열처리공정 중 요동을 일으키는 원인이 된다. 시뮬레이션은 이와 같이 용기의 형상의 변화와 같은 형상인자의 변화에 따른 열처리조건의 변화를 예측하는데 매우 유용하게 사용될 수 있다. 원통형 용기와 원뿔형 용기 내의 비뉴턴성 유체의 SHZ의 위치 변화가 시뮬레이션에 의하여 해석되었다(Varma and Kannan, 2006). 이 연구는 용기의 형상과 함께 용기의 방향도 열전달 효율에 매우 큰 영향을 주며 살균도의 계산에 반영되어야 함을 보고하였다. Boz and Erdogdu (2013)는 2차원 모델링을 통하여 원통형 용기가 수평인 방향성을 지닐 경우의 온도분포와 속도분포를 계산하였다. 이와 같은 방향성에 대한 효과는 맥주캔의 방향성에 따라 살균공정의 효율의 변화에 대해서도 연구되고 보고되었다(Augusto et al., 2010). 맥주캔을 정상적으로 세워놓은 경우, 뒤집어 놓은 경우, 수평으로 놓은 경우에 대하여 시뮬레이션을 수행하였으며 이와 같은 방향성에 따라 온도분포와 흐름의 분포가 크게 차이가 남을 보여주었다. 결론적으로 유체의 특성에 따라 에너지수지식과 운동량수지식을 이용하여 얻은 온도와 속도 분포는 유체의 특성뿐만 아니라 외부적인 요소인 용기의 형상과 방향성에도 크게 영향을 받게 된다.
액상과 고체상이 혼합된 식품
액상의 식품의 열전달은 자연 대류가 주요한 기작임에 반하여 액상-고상 혼합물의 고체식품의 경우 전도가 주요한 기작으로 작용한다(Kumar et al., 1990). 그러나 일반적으로 가열살균시간의 계산은 일방적으로 열전달은 전도기작만이 있다는 비현실적인 가정을 토대로 이루어진다. 이와 같은 현실적이지 못한 가정은 대류에 의한 열전달효과를 무시한 체로 가열살균시간이 계산되므로 실제 필요한 가열시간 보다 긴 시간을 추정하게 된다. 이와 같은 필요 이상으로 긴 가열시간의 적용은 궁극적으로 과살균이 되므로 제품의 품질에 변화를 주게 되고 생산성과 에너지의 효율적 사용에 영향을 주게 된다(Naveh et al., 1983).
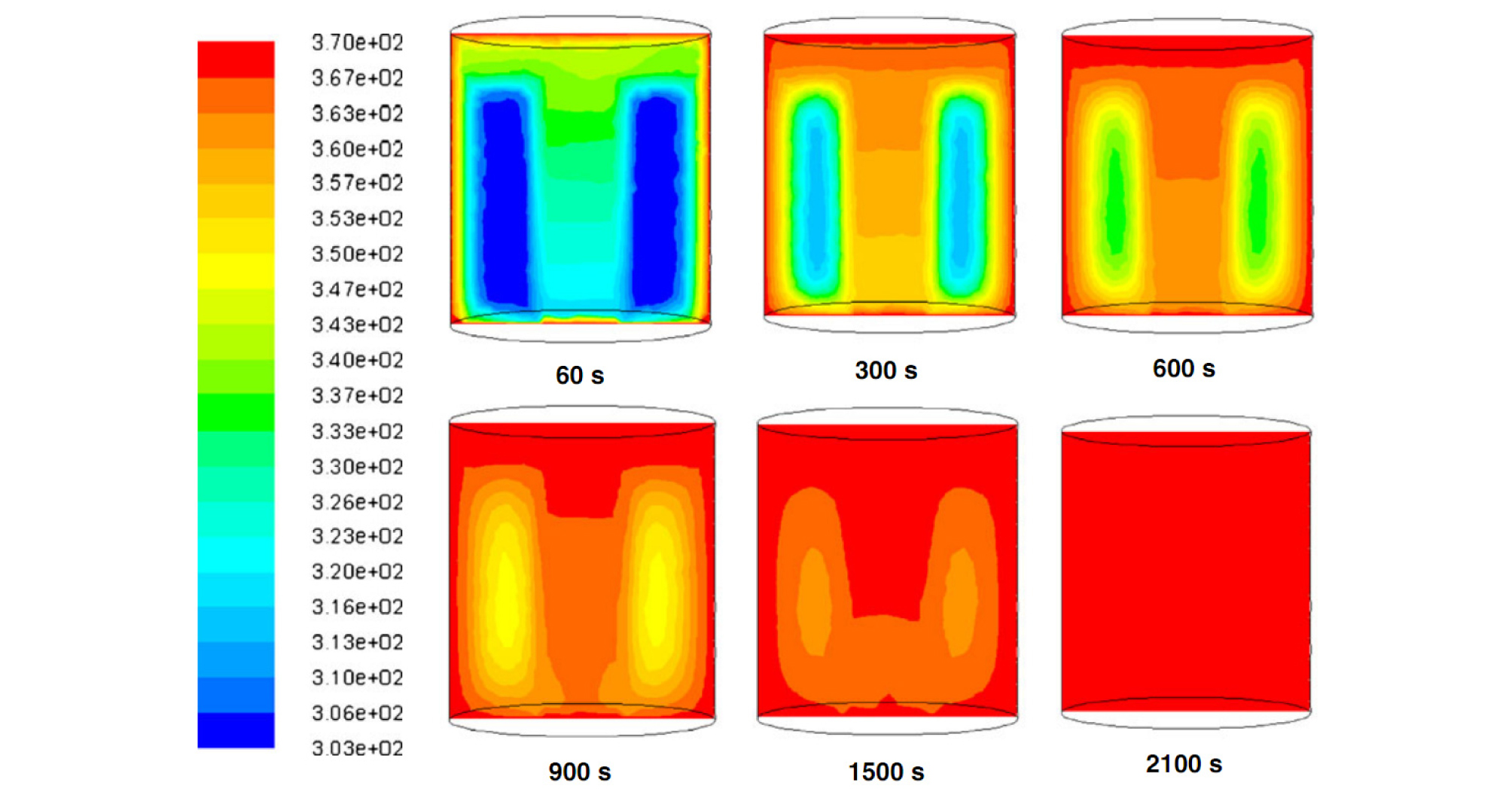
최근 시뮬레이션을 통한 가열공정의 해석은 액상-고상 혼합물에 대한 적용으로 확장되고 있다. 액상-고상 혼합물의 열처리 시에 적용되는 시뮬레이션의 주된 목적은 액체내의 고체식품이 SHZ의 위치변화에 미치는 영향과 용기내의 유체의 흐름을 해석하는 것이다. 액상 식품과 달리 액상-고상 혼합물의 경우 대류와 전도 모두가 주요한 열전달 기작으로 작용하므로 이에 따른 해석이 필요하다(Dimou and Yanniotis, 2011; Cordioli et al., 2015; Dimou et al., 2013; Padmavati and Anandharamakrishnan, 2013). 파인애플을 슬라이스 한 조각들을 설탕용액과 함께 원통형 용기에 포장 후 가열 살균을 하는 경우 유체의 흐름과 온도분포를 해석하기 위하여 파인애플 슬라이스에 대해서는 전도기작을 적용시키고 설탕용액에 대해서는 자연대류를 적용시켜 시뮬레이션을 진행하여 해석한 연구가 보고된 바가 있다(Ghani and Farid, 2006). Padmavati and Anandharamakrishnan (2013)도 파인애플 슬라이스와 설탕용액에 대한 시뮬레이션을 진행하여 SHZ가 용기의 중심부인 유체에 존재하지 않고 고체상인 파인애플에 위치함을 보고하였다(Fig. 5). 일반적으로 과일의 통조림에 담금액으로 사용하고 있는 설탕용액의 농도는 16.7%이며, 이와 같은 설탕용액은 액상-고상 혼합물 중 액상이 차지하는 비율이 40% 이하가 되더라도 살균도(F-value)는 설탕용액의 자연대류에 의하여 유의미한 변화를 가져옴을 보여 주었다(Cordioli et al., 2015). 원통형 용기의 방향성은 액상-고상혼합물에서도 매우 큰 영향을 보여 주었으며 수직형인 경우가 가장 열전달 속도가 늦은 것을 보여 주었다(Dimou et al., 2014). Dimou and Yanniotis (2011)는 아스파라가스가 담금액에 담가 있는 상태의 열처리 과정 중의 온도와 흐름분포에 대한 시뮬레이션을 진행하였으며 용기 내의 아스파라가스가지의 개수가 유체의 흐름에 유의미한 영향을 주는 것을 확인하였다. 액상-고상의 혼합물의 SHZ의 위치는 단일 액상에 비하여 변화가 매우 크며 여러 변수에 의하여 영향을 받게 된다. 이는 고형분이 용기 안에 있으므로 유체의 흐름을 방해하는 역할을 하므로 생기는 현상으로 일반적으로 SHZ는 순수한 액상보다 위쪽 방향으로 이동하게 된다. 또한 SHZ는 액상보다는 고체성분 중의 특정 위치에서 발견되며 이는 고체성분이 액체보다 내부 열저항이 크기 때문이다.
가열 살균공정에서의 시뮬레이션의 한계와 미래
현재 산업화된 규모의 가열살균기(예, 레토르트)를 설계하거나 운전하는 경우 컴퓨터 시뮬레이션을 통한 설계요소를 선정하고 평가하여 설계에 반영하는 것은 필수적인 설계 과정 중의 하나이다. 이는 산업화된 대용량의 살균기는 매우 복잡한 구조를 가지고 있으며 해석적인 해를 바탕으로 설계하고 운전한다는 것은 매우 어렵기 때문이다. 용기 내의 식품의 가열 처리에 대한 시뮬레이션을 통한 해석은 다양한 연구를 통하여 진행되었으며 성공적인 결과를 가져오고 있으나, 현재에도 대용량 살균기를 설계하는데 시뮬레이션을 사용하는데는 한계점이 존재한다. 대표적인 한계점은 1)스팀의 유동을 반영하는 것, 2)증발-응축의 상변화를 반영하는 것, 3)파우치 용기의 팽창을 반영하는 것이다. 대용량 살균기 내부의 온도편차와 증발-응축의 상변화는 살균기 설계와 해석에서 실질적인 어려움을 주는 부분이다. 특히 이와 같은 현상을 시뮬레이션 할 수 있는 상용화된 시뮬레이션 소프트웨어가 존재하지 않는 다는 어려움도 있다. 이를 해결하기 위하여 ANSYS나 COMSOL의 경우 사용자 지정 함수(user defined function, UDF)를 사용자가 개발하여 상용화된 소프트웨어와 연동하여 계산할 수 있도록 하고 있다.
시뮬레이션의 또다른 한계점은 현재 가열살균과 비가열 살균이 혼합되어 있는 복합공정이 존재하는데 이와 같은 공정에 시뮬레이션을 적용하기가 어렵다는 것이다. 예를 들면 가열살균공정과 함께 초고압, 초음파, 적외선복사열전달을 사용하는 경우가 최근 등장하는 새로운 살균공정이며 이는 기존의 전통적인 가열살균공정에 적용하던 시뮬레이션방법을 적용하여 현상을 해석하는데 한계점을 부여하고 있다.
현재 상용화된 소프트웨어의 발전속도와 컴퓨터 하드웨어의 발전속도를 감안할 시 계산능력의 지수적인 성장으로 지금보다 복잡한 시뮬레이션도 해결이 가능할 것으로 예상되며, 특히 대용량의 산업화된 규모의 살균장비의 설계와 운전에 고성능의 계산기능이 적용되어 현재보다 정교한 해석을 얻으리라 예상한다.
결 론
본 총설논문의 목적은 현재 가열살균에 사용되는 시뮬레이션 방법을 식품에 적용되는 대표적인 열전달 기작: 1)전도열전달 기작(고체 또는 고점도 유체식품), 2)대류 열전달 기작(액상의 식품), 3)전도-대류 혼합 연전달 기작(액상-고상 혼합 식품)으로 구분하여 소개하였다. 고체식품의 CP는 기하학적 중심에 위치하여 설정하기가 비교적 용이하나 액상의 경우 SHZ는 유체의 다양한 특성과 형상과 방향성에 의존하므로 시뮬레이션을 통하여 그 위치의 추적이 가능하다. 액상-고상 혼합인 식품의 경우 대류와 전도가 동시에 작용하는 복잡한 기작으로 SHZ의 예측은 고체성분의 특성과 함께 액상의 점도 등에 의하여 결정된다. 본 총설에서는 현재 가열살균에 적용되는 시뮬레이션의 한계인 대용량 살균기의 설계와 운전 및 가열-비가열 혼합공정에 대해서도 소개하였다.



 velocity component (m s-1)
velocity component (m s-1)
